Ever listen to classical music and feel like something is just a little bit off?
You’re not crazy. That slightly jarring feeling you get when listening to classical music is called dissonance, and it’s one of the most important tools composers use to create emotion in their music.
Dissonance can be used to evoke feelings of tension, suspense, horror, or even sadness. It’s an essential tool for any composer looking to create a truly memorable musical experience.
Make sure to read the complete article to get valuable insights about dissonance and consonance in classical music!
Consonance vs. Dissonance in music. What Does Dissonance Mean?
You would have heard the music that sounds good, pleasing or sweet, very easy to listen, one that sounds like resolution and tends towards reduced tension. On the other end of the spectrum is the music that heightens the tension and is made up of sounds that appear surprising, difficult, or outright harsh to the audience.
The first one provides the listener with the feeling of stability and repose, while the other one generates the impression of tension or clash. These are the feelings evoked by successive or simultaneous sounds.
The above description of consonance and dissonance makes the two sounds feel like the exact opposite or mutually exclusive of each other. In actual music, a gradation exists from one extreme to the other. Only consonant music will appear dull after some time. The presence of both dissonant and consonant sounds provides shape, direction, and movement in music by playing with the levels of tension before finally releasing it.
However, as per the Wundt Curve, there has to be a balance between predictability and complexity. Both extremes are not preferred. The sweet spot between the two is usually governed by an inverted U-shaped curve that peaks in the middle. The peak position may vary a bit based on individual perceptions, but the pattern remains consistent for most listeners.
In the next few sections, we will look through the acoustics and physics behind the two in simple terms so that you can appreciate the subsequent discussions.
What Is Consonance in Music?
Humans are blessed with the ability to produce sounds in discrete pitches while speaking or singing. These discrete pitches get organized in patterns the brain can recognize and interpret. The brain is hardwired to recognize certain ordered relationships between the tones and rejects the balance as noise.
This ordered relationship between the tones translates to the melodic intervals in music. You learned from one article on “guitar scales” that scales are defined by the set of intervals between the notes. Also, in our article on “guitar intervals,” you noted that interval is a relation between two notes with a unique sound and a measure of harmonic distance between them.
Those were subjective discussions. Let us understand the relationship objectively; what are consonant and dissonant sounds, consonant and dissonant intervals, and how are they defined in music theory?
Overtones and Simple Ratios
You would have played the notes of a chromatic scale. How did you find them? All the notes in the chromatic scale are evenly spaced and hence do not provide any musical value to the brain. Similarly, try generating a single-frequency sound on your PC. Again, it is devoid of any musical value.
If you pick any open string on your guitar, it appears interesting due to the presence of the overtones or harmonics. These overtones define the characteristics of any musical instrument, a property known as timbre. The relationship between the notes of melodic intervals that define their musical characteristics of any interval is also governed by the overtones and their inter-relationship or ratios. Let us see this in detail.
The Overtone Ratios
Let us start with the note C3 on the piano, having a fundamental frequency of 130.8 Hz, and list down its overtones and calculate the frequency ratios. You must start by taking the frequency ratios with the fundamentals. Once we reach an octave frequency, we will use it to take the ratio for further overtones, and so on. The results are presented in the table below for the first five overtones.
| Overtone No. | Freq Multiple | Freq Ratio | Actual Frequency in Hz |
|---|---|---|---|
| Fundamental | 1F | 1:1 | 130.8 |
| First Overtone | 2F | 2:1 | 261.6 |
| Second Overtone | 3F | 3:2 | 392.4 |
| Third Overtone | 4F | 2:1 | 523.2 |
| Fourth Overtone | 5F | 5:4 | 654.0 |
| Fifth Overtone | 6F | 3:2 | 784.8 |
We see that the overtones present simple ratios of 2:1, 3:2, and 5:4, with the fundamental and its octaves.
The ratio between Notes of a Major Scale
You know that the major scale has contributed to the maximum number of musical pieces in Western music. You must look at the frequency ratios between its notes to derive some inference about the consonant intervals in popular music. The frequency of the notes of the C Major scale in one octave starting from the C4 note (middle C in piano) is shown in the table below.
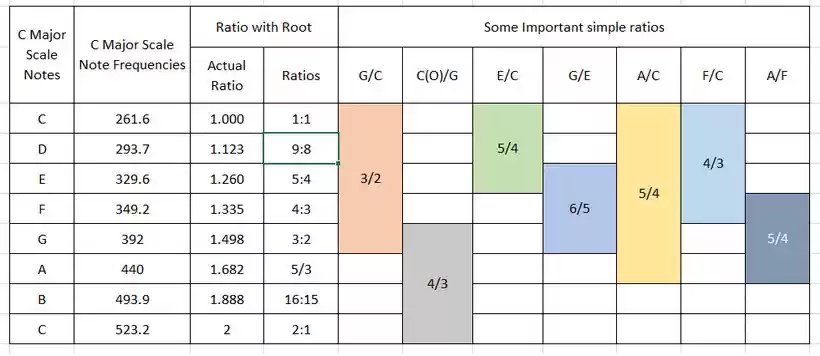
From the table, you can observe the ratio of frequencies of different notes with the tonic. In particular,
- The scale degree 3 has a ratio of 4:3 with the tonic note.
- Scale degree 5 has a ratio of 3:2
- Scale degrees 2 and 7 have a ratio of 9:8 and 16:15 with the tonic.
You must have frequently heard that the scale degrees two and seven of a major scale represent dissonant intervals that want to resolve to the tonic badly. What makes them produce a dissonant sound?
If you observe the ratios carefully, you will find that all other ratios, except these two, are simple ratios. The scale degree 7, representing the major seventh, is also known as the leading tone and has the most complex ratio of 16:15. The scale degree 2 (a Major 2nd) is next in complexity with a ratio of 9:8
What appears from the above is the simple ratios sound consonant to the brain, while the complex ones are dissonant. This means that you must categorize all the intervals that you commonly encounter in music theory into consonant or dissonant intervals.
All Intervals of a Diatonic Scale
As stated in the previous section, a dissonant interval has complex ratios, while a consonant interval has simpler ones. The table below shows the ratios for all the diatonic intervals, along with categorization into consonant and dissonant intervals.
These are summarized below:
| Interval Name | Semitones | Interval Notes | Ratio | Type |
|---|---|---|---|---|
| Perfect Unison | 0 | C - C | 1:1 | Consonant |
| Minor Second | 1 | C - C# | 16:15 | Dissonant |
| Major Second | 2 | C - D | 9:8 | Dissonant |
| Minor Third | 3 | C - D# | 6:5 | Consonant |
| Major Third | 4 | C - E | 5:4 | Consonant |
| Perfect Fourth | 5 | C - F | 4:3 | Consonant |
| Augmented Fourth | 6 | C - F# | 45:32 | Dissonant |
| Perfect Fifth | 7 | C - G | 3:2 | Consonant |
| Minor Sixth | 8 | C - G# | 8:5 | Consonant |
| Major Sixth | 9 | C - A | 5:3 | Consonant |
| Minor Seventh | 10 | C - A# | 9:5 | Dissonant |
| Major Seventh | 11 | C - B | 16:15 | Dissonant |
| Perfect Octave | 12 | C - C (O) | 2:1 | Consonant |
- Perfect Consonant Intervals: Unison and Octaves.
- Median Consonant Intervals: Perfect Fourth and Perfect Fifth.
- Imperfect Consonant Intervals: Major Third, Minor Sixth, Minor Third, and Major Sixth.
- Imperfect Dissonant Intervals: Major Second, and Minor Seventh.
- Perfect Dissonant Intervals: Augmented Fourth, also known as Tritones, Minor Second, and Major Sevenths,
You can see that the complementary intervals fall in the same category, except for the tritone, which does not have a complement.
In simple terms, intervals are considered consonant if they have overtones and overlapping sounds, while dissonant intervals don’t have them or have them in much lesser proportions.
This leads us to the other dimension, that consonance also depends on the combined spectral density and sound quality, also known as the timbre, discussed earlier. The timbre of any instrument is a function of the overtones produced by it and hence contributes to the consonance of notes.
If you really want to dig deep into the subject, then other aspects like coincidence of partials, dynamic tonality, etc, also come into play, but you don’t require to bother yourself with them, and you can limit yourself to the ratios only.
What Is Dissonance in Music & Its Causes?
By now, you have a fair idea of how to define dissonance and know its causes. In addition, some musicians also use the term for the combination of sounds that do not belong to the style under consideration. These discordant sounds may be defined as stylish dissonance against the acoustic dissonance that we discussed above.
Tonal music is defined as one based on the 24 diatonic keys, equal temperament, and tonality. Everything that goes into establishing a tonal center is called tonality. This includes the organized relationships of pitches around the tonal center, including the key, the relation of scale, and chords to the key. Tonal music relies on both consonance and dissonance.
Atonal music, on the other hand, does not have a tonal center. Developed by the Austrian composer Arnold Schoenberg and based on what is known as the serial system, this music gives the same importance to every note so that the listener cannot recognize any tonal center.
This results in the practical exclusion of small ratio intervals in both the harmony and melody, breeding dissonance.
Consonance & Dissonance in Harmony
So far, you have seen what causes consonance and dissonance in melody. Let us now dwell upon the reasons that impact them in harmony in your music. Yes, you guessed it right. It has again to do with the overtones. However, we will deal with the scale degrees associated with the overtones instead of the overtones themselves. Take a look at the table below.
| Overtone No. | Freq Multiple | Freq Ratio | Scale Degree | Note | Consonant? |
|---|---|---|---|---|---|
| Fundamental | 1F | 1:1 | 1 | C | Yes |
| 1st Overtone | 2F | 2:1 | 1 | C | Yes |
| 2nd Overtone | 3F | 3:2 | 5 | G | Yes |
| 3rd Overtone | 4F | 2:1 | 1 | C | Yes |
| 4th Overtone | 5F | 5:4 | 3 | E | Yes |
| 5th Overtone | 6F | 3:2 | 5 | G | Yes |
| 7th Overtone | 8F | 2:1 | 1 | C | Yes |
| 9th Overtone | 10F | 5:4 | 3 | E | Yes |
You can see that the major overtones of C, the tonal center in the C major scale — the 1st, 2nd, 3rd, 4th, 5th, 7th, and 9th overtones are associated with the pitches of the scale degrees 1, 3, and 5. These notes form the C major chord when played simultaneously.
From the last discussion, you noted that playing any note reinforces its scale degrees 1, 3, and 5. Since you are playing three notes simultaneously in a chord, this reinforcement happens for every note. Hence,
| Overtone No. | Freq Multiple | Freq Ratio | Scale Degree | Note C | Note E | Note G |
|---|---|---|---|---|---|---|
| Fundamental | 1F | 1:1 | 1 | C | E | G |
| First Overtone | 2F | 2:1 | 1 | C | E | G |
| Second Overtone | 3F | 3:2 | 5 | G | B | D |
| Third Overtone | 4F | 2:1 | 1 | C | E | G |
| Fourth Overtone | 5F | 5:4 | 3 | E | G# | B |
| Fifth Overtone | 6F | 3:2 | 5 | G | B | D |
- The three notes associated with C major triad appear as overtones of C.
- Both the other tones, E and G, have B as the overtone, which corresponds to the 7th scale degree of C Major, known as the leading tone that points strongly to C.
- The other overtones are D and G#. D belongs to scale degree 2, which again points strongly to C, while G# wants to resolve to G.
Hence all the overtones of the three notes work together to reinforce each other and the tonal centers, a phenomenon known as resonance. This is why major triads are very balanced, stable, and sound good.
Consonant Intervals Form Consonant Harmony
If all the intervals (internal and outer) are consonant, the chord will be consonant. Even one dissonant interval will result in dissonant chords and harmonic intervals. Let us consider this with some examples:
- A major triad has intervals of a major third and a minor 3rd stacked over the root. These intervals are called internal intervals. The interval between the root and the top note is a perfect fifth, known as the outer interval. All three associated intervals (major 3rd, minor 3rd, perfect 5th) are consonant intervals, resulting in a consonant chord.
- Any minor chord has the same internal intervals, although inverted, and the same outer interval. Hence these chords are also consonant.
- Any diminished chord has two minor 3rds stacked over the root, which is consonant intervals. But, the outer interval is an augmented fourth (the tritone) with the most complex ratio of all the intervals, making it a dissonant chord.
With the ongoing discussion, what do you think an augmented chord with all three consonant intervals (major 3rd, major 3rd, and minor 6th) is?
It will give rise to a dissonant chord. Why?
This is because dissonance and imbalance also result if you divide the complete octave into either a large number of small equal intervals or a small number of large equal intervals. Hence, two major thirds or ditonic intervals stacked over each other result in dissonance. The same thing happens when four equal minor thirds are formed from an octave.
All 7th chords, extended and altered chords, are dissonant, as they contain a 7th interval, which is dissonant. What about a suspended chord? It carries a major 2nd interval.
Why Do Composers Use Dissonance?
Composers make use of dissonance in musical composition as it is one of the tools to create movement, change, rising and falling action, a sense of urgency, and build tension followed by a period of release. Particularly, jazz and classical musicians frequently use it to evoke strong emotions among listeners.
As per the reference in music history, the terms tension and relaxation were used to describe the alternate use of dissonance and consonance to provide the movement and direction to the music.
Conclusion
Music is often seen as pleasant and relaxing, but there is another element to it that can create suspense, unease, and sometimes even fear. This element is called dissonance, and in this blog post, we explored what it is, why composers use it, and how it differs from consonance. We also looked at some examples of dissonance in classical music. If you have any questions or would like clarification on anything, feel free to let me know in the comments section below.

